傳統數字濾波器硬件的實現主要采用專用集成電路(ASIC)和數字信號處理器(DSP)來實現。FPGA內部的功能塊中采用了SRAM的查找表(lo-ok up table，LUT)結構，這種結構特別適用于并行處理結構，相對于傳統方法來說，其并行度和擴展性都很好，它逐漸成為構造可編程高性能算法結構的新選擇。
分布式算法是一種適合FPGA設計的乘加運算，由于FPGA中硬件乘法器資源有限，直接應運乘法會消耗大量的資源。本文利用了豐富的存儲器資源進行查找表運算，設計了一種基于分布式算法低通FIR濾波器;利用線性相位FIR濾波器的對稱性減小了硬件規(guī)模;利用分割查找表的方法減小了存儲空間;采用并行分布式算法結構和流水線技術提高了濾波器的速度，在FPGA上實現了該濾波器。
1 分布式的濾波器算法
FIR濾波器突出的特點是單位取樣響應h(n)僅有有限個非零值。對于一個N階的FIR濾波器形式如下：
在許多數字信號處理應用領域中，在技術上是不需要通用的乘法算法的。對于本系統可以通過Matlab中的fdatool工具根據設計要求設計出濾波器的系統函數h(n)，那么乘積項h(k)×x(n-k)就變成了2個常數的乘法。無符號數的分布式算法和有符號數的分布式算法是分布式算法在FIR濾波器中的2種典型算法。
1.1 無符號數的分布式算法設計
由于FPGA為并行處理結構，所以假設x(n-k)數據寬度為L b，則由式(1)可表示為：
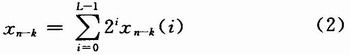
由式(1)、式(2)可以得到：
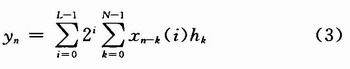
假設：
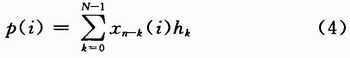
則式(1)可以表示為：
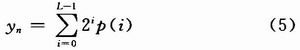
1.2 有符號數的分布式算法設計
對于有符號數的補碼表示為：
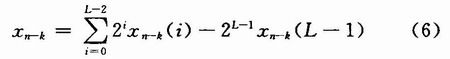
則由式(5)，式(1)可得：
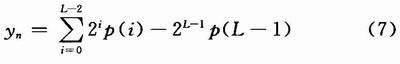
2 分布式的濾波器的軟件實現
從式(5)和式(7)可以看出，利用分布式算法實現一個N項乘積和，關鍵是如何實現式(4)中乘積項及各乘積項之和。
在FPGA中可以預先設定一個N位輸入的查找表來實現部分乘積項，即預先設定N階濾波系統查找表，實現向量x(i)={x0(i)，x1(i)，x2(i)，…，xN-1(i))到p(i)的一個映射。由于查找表的地址空間與階數成指數關系(2N)，完全用查找表來實現部分乘積項需要容量很大的存儲器，這就需要占用巨大的資源，而且功耗增加、速度降低。因此為了減小設計規(guī)模，可以將一個大的查找表分為幾個較小的查找表來實現。例如，本系統采用的8階FIR濾波器，則用一個查找表來實現需要256(28)位地址空間的ROM，將8階FIR濾波器分成兩個4階FIR濾波器實現，只需要2個16(24)位地址空間的ROM，這樣大大地降低了設計規(guī)模和資源使用量。把輸入x(i)作為地址，分為高四位和低四位地址進行查找。
實驗結果表明，基于分布式算法低通FIR濾波器的優(yōu)點是工作可靠，濾波精度較高，且具有占用資源少，運算速度快。在資源允許的條件下可根據實際應用任意確定濾波器的字長和階數，在高速數字信號處理領域可以得到很好的應用。
